
- Special right triangles side lengths how to#
- Special right triangles side lengths plus#
- Special right triangles side lengths series#
of the leg which is 7 inches by 2 to get the length of the hypotenuse. Start working on your geometry questions, and next time we'll go over polygons and the dreaded circle. There are a couple of special types of right triangles, like the 45-45 right. Similarly, a right triangle with a hypotenuse of 13 and a smallest side of 5 MUST have a side of length 12. They are:Īny right triangle with short sides of lengths 3 and 4 MUST have a hypotenuse of 5. Some right triangles feature easily-recognizable sequences of side lengths (remember: this is ONLY for right triangles!). Let the shortest side be called “X.” The hypotenuse will be twice as long, or 2X, while the remaining side will be X√3. In that case, we take the √2 and place it under the “X” as the denominator this can be expressed as X/√2. Sometimes, the test makers will try to throw you off by giving you the hypotenuse and not the sides. We can call them “X.” The hypotenuse will always be X√2. The two sides opposite the 45 degree angles will always be equal. (The word “hypotenuse” literally means "longest side" in Greek.) With the knowledge of any two of the sides of a right triangle, the third can be derived using Pythagoras' theorem.īut what's a special right triangle? There are two you'll need to be familiar with for the GRE: the 45-45-90 triangle, and the 30-60-90 triangle.Ī 45-45-90 triangle is a right isosceles triangle. The hypotenuse is the side opposite the 90 degree angle, and will always be the longest of the three sides.

Special right triangles side lengths plus#
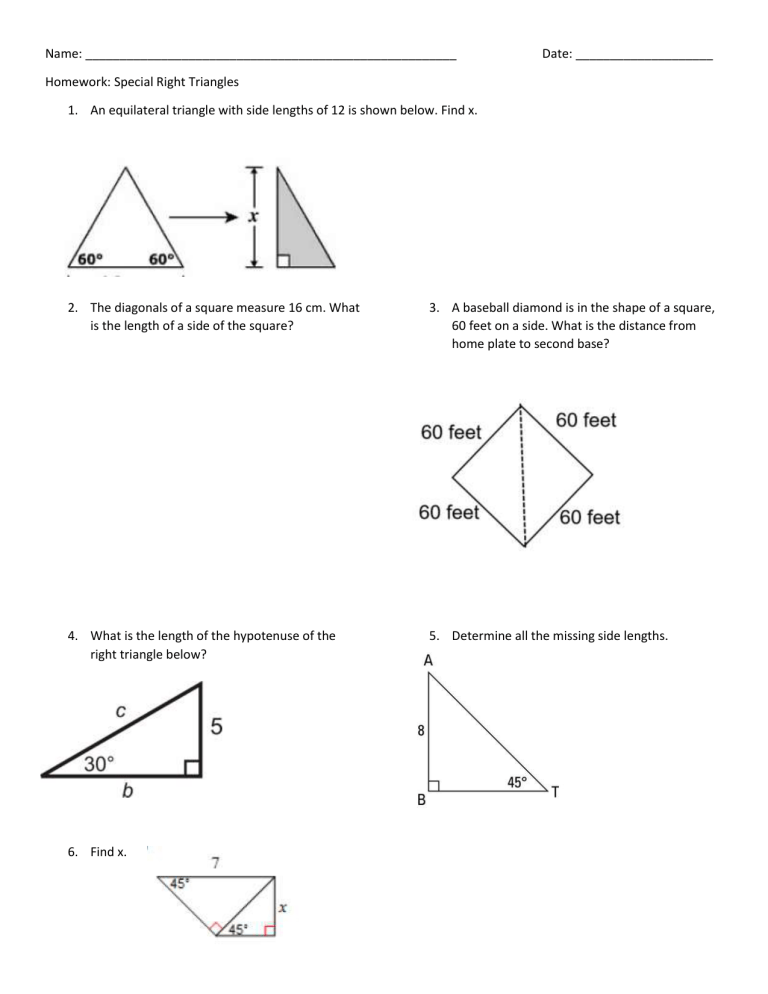
Put simply: the square of side A plus the square of side B will equal the square of the hypotenuse. Pythagoras was a Greek mathematician who discovered the rules of right triangles. Again, unless you see that blue drawing or it is expressly stated in the question, do not assume an angle is 90 degrees.) (Note the blue square: that’s the GRE's way of telling you that the angle is 90 degrees. If it is a right triangle, however, the Pythagorean theorem will surely come into play. Never assume a triangle is a right triangle unless the problem states that it is. Let's start by defining our terms: a right triangle is one in which one of the sides equals 90 degrees. Fill in the length of each segment in the following figures. 450 45 Period: Name: Isosceles Right Triangles Assignment r. Leave your answers as radicals in simplest form. The height is a straight vertical line from the base to the vertex. Special Right Triangles Name Date Period. To determine your base, rotate the triangle in your mind to where the longest side would be flat along the ground. To find the perimeter of a triangle, simply add up the lengths of the sides.įor area, we multiply the length of the base times the height and divide by two, or 1/2(bh). The longest side is opposite the largest angle, and the shortest side will be opposite the smallest angle. There are three different kinds of triangles: scalene (all side lengths and angles are different) isosceles (two sides and angles are the same) and equilateral (all three sides are the same length, and all angles are 60 degrees each. Triangles are polygons with three sides the sum of their interior angles add up to 180 degrees.
Special right triangles side lengths how to#
Let’s talk about some of the more common shapes on the GRE geometry section and how to deal with them. Add a third line and you've got a shape called a triangle. If the two lines meet at a right angle, they are called perpendicular if the two lines run next to each other and will never meet, they're called parallel (do not assume that lines on the test are perpendicular or parallel unless the problem states that they are!). Add another line, and where the two meet is called an angle. On the GRE, all lines that appear straight are straight.
Special right triangles side lengths series#
Lines are infinitely thin, infinitely long series of points. Explanation: To find the length of the missing side, you can either use the pythagorean theorm or realize this is a case of a special right triangle with sides. That's all geometry is: lines, angles, and shapes (it's coming back to you, isn't it?). Exploration: Consider an isosceles right triangle, with each side of 1 cm, as shown. Let's review what you'll need to know about triangles for the GRE. Students will be able to find missing sides of special right triangles. The bad news is that you may have forgotten a lot of what you learned in those classes. The good news is that the GRE usually doesn't test any concepts you wouldn't have learned in high school. If you're like most students preparing to take the GRE, you haven’t taken a math class in a few years.


 0 kommentar(er)
0 kommentar(er)
